 |
|
Please Whitelist This Site?
I know everyone hates ads. But please understand that I am providing premium content for free that takes hundreds of hours of time to research and write. I don't want to go to a pay-only model like some sites, but when more and more people block ads, I end up working for free. And I have a family to support, just like you. :)
If you like The TCP/IP Guide, please consider the download version. It's priced very economically and you can read all of it in a convenient format without ads.
If you want to use this site for free, I'd be grateful if you could add the site to the whitelist for Adblock. To do so, just open the Adblock menu and select "Disable on tcpipguide.com". Or go to the Tools menu and select "Adblock Plus Preferences...". Then click "Add Filter..." at the bottom, and add this string: "@@||tcpipguide.com^$document". Then just click OK.
Thanks for your understanding!
Sincerely, Charles Kozierok
Author and Publisher, The TCP/IP Guide
|
|
|

Custom Search
|
 |
The TCP/IP Guide 9 Networking Fundamentals 9 Backgrounder: Data Representation and the Mathematics of Computing |
|
Binary Information and Representation: Bits, Bytes, Nibbles, Octets and Characters
(Page 2 of 3)
Binary Information Representation and Groups
The fundamental building block of computer information is the bit (a contraction of binary digit). Every bit can be either 0 or 1. Making the value of a bit 1 is commonly called setting the bit; changing it to 0 is resetting or clearing it.
Of course, bits represent only a very small amount of information: a single fact or value. We must make collections of these bits so we can use them to store large amounts of information and more complex data types. The most common grouping is to take eight bits and reference them as a single unit. A collection of eight bits is technically called an octet, but is more commonly called a byte. (More on that in a moment.)
“Byte” is a jocular play on the term “bit”. Over time, other sizes of “bit collections” have also been defined. Some geek comedian decided that if eight bits made a “byte”, then four bits must be a “nybble” (or “nibble”). Hilarious. J Larger collections have also been defined and given various names. Table 1 summarizes the most common representations of groups of bits, and the terms used for them; their relative sizes are also shown graphically in Figure 8.
Number of Bits |
Common Representation Terms |
1 |
Bit / Digit / Flag |
4 |
Nybble / Nibble |
8 |
Byte / Octet / Character |
16 |
Double Byte / Word |
32 |
Double Word / Long Word |
64 |
Very Long Word |
A few of these terms are worth special mention. Bit and byte we have already discussed, of course. A bit is also sometimes called a flag; this term is most often heard when a bit is used by itself to represent a particular information state. For example, a computer might use a “changed flag” to represent whether a particular file has been modified; this is an analogy to a flag either being raised or lowered to indicate a condition. These “flags” are often seen in networking message formats.
The term character is also used to express a set of eight bits. This use comes from the fact that computers often store alphanumeric characters, such as letters and numbers, one to a byte. The 16-bit word is fairly often used, but not nearly as much as “byte”. The larger collections of bits, such as double word and so on, are not often encountered in every-day parlance; they are used to represent chunks of data in technical fields such as hardware design or programming.
|
You may also have noticed the number of bits used for each of these terms is a power of two. This is of course not a coincidence. As we will see in the subsequent topics in this section, this occurs because when bits come in sets that are a power of two in size, they are easier to represent and manipulate in a convenient manner. The number of bits in the term can itself be easily expressed using binary numbers. This will make more sense after you read the topic that follows on decimal binary, octal and hexadecimal numbers.
|
|
| |||||||||||||||||||
Home - Table Of Contents - Contact Us
The TCP/IP Guide (http://www.TCPIPGuide.com)
Version 3.0 - Version Date: September 20, 2005
© Copyright 2001-2005 Charles M. Kozierok. All Rights Reserved.
Not responsible for any loss resulting from the use of this site.






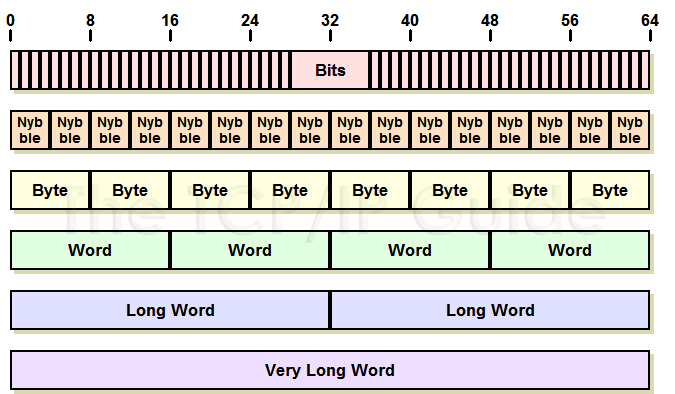
 Key Concept: Computers store all information in binary digital form, which means all data—be it text, photographs, audio or whatever else—is comprised only of collections of ones and zeroes. The fundamental building block of digital information is the binary digit or bit, which represents a single zero or one state. To represent larger amounts of information, bits can be collected into groups of four, eight, sixteen, 32 or 64, called nybbles, bytes, words, long words and very long words respectively.
Key Concept: Computers store all information in binary digital form, which means all data—be it text, photographs, audio or whatever else—is comprised only of collections of ones and zeroes. The fundamental building block of digital information is the binary digit or bit, which represents a single zero or one state. To represent larger amounts of information, bits can be collected into groups of four, eight, sixteen, 32 or 64, called nybbles, bytes, words, long words and very long words respectively.