Please Whitelist This Site? I know everyone hates ads. But please understand that I am providing premium content for free that takes hundreds of hours of time to research and write. I don't want to go to a pay-only model like some sites, but when more and more people block ads, I end up working for free. And I have a family to support, just like you. :) If you like The TCP/IP Guide, please consider the download version. It's priced very economically and you can read all of it in a convenient format without ads. If you want to use this site for free, I'd be grateful if you could add the site to the whitelist for Adblock. To do so, just open the Adblock menu and select "Disable on tcpipguide.com". Or go to the Tools menu and select "Adblock Plus Preferences...". Then click "Add Filter..." at the bottom, and add this string: "@@||tcpipguide.com^$document". Then just click OK. Thanks for your understanding! Sincerely, Charles Kozierok Author and Publisher, The TCP/IP Guide

NOTE: Using software to mass-download the site degrades the server and is prohibited. If you want to read The TCP/IP Guide offline, please consider licensing it. Thank you.

The TCP/IP Guide  9  Networking Fundamentals       9  Backgrounder: Data Representation and the Mathematics of Computing

Binary Information and Representation: Bits, Bytes, Nibbles, Octets and Characters 1 2 3 Decimal, Binary, Octal and Hexadecimal Number Conversion

Making Binary Numbers Easier to Use By Grouping Bits

One problem with binary numbers is that while computers love them, they are unintuitive for humans, who are used to decimal numbers. One reason for this is that they quickly get very, very long and cumbersome to deal with. For example, 1,000,000 in decimal is 11110100001001000000 in binary. To make binary numbers easier to work with, two different shorthand notations have been defined. In both of these, instead of working with each bit individually, they are collected into subgroups, each of which is assigned a single digit in an alternative numbering system.

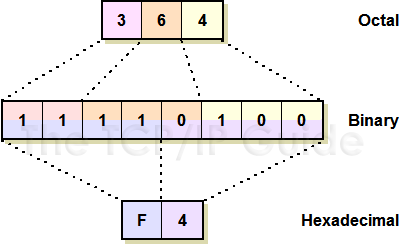
Let's take the binary number 11110100, which is 244 in decimal. Now, instead of looking at each bit individually, let's chop them into groups of three, starting from the right. So, 11110100 becomes (11)(110)(100). Now, each of those groups has three bits, so each can have 2³ values: from 0 to 7. In this case, (11)(110)(100) = (3)(6)(4), or 364 in the octal or base-8 numbering system (see Figure 9). Just as with binary, octal numbers are the same as decimal numbers, except they are base 8 instead of base 10. So, 364 in octal is just 3 times 64 plus 6 times 8 plus 4, or 244. The advantage that octal has over binary is obvious: it's a lot less cumbersome to deal with larger numbers. 1,000,000 in decimal is 3641100 in octal.

Figure 9: Binary, Octal and Hexadecimal Number Representations

A binary number can be represented in octal form by grouping its bits into sets of three, or in hexadecimal by using sets of four bits. These base-8 and base-16 numbers have the advantage of being far shorter than binary numbers, and hence much easier to work with.

Binary Information and Representation: Bits, Bytes, Nibbles, Octets and Characters 1 2 3 Decimal, Binary, Octal and Hexadecimal Number Conversion

If you find The TCP/IP Guide useful, please consider making a small Paypal donation to help the site, using one of the buttons below. You can also donate a custom amount using the far right button (not less than $1 please, or PayPal gets most/all of your money!) In lieu of a larger donation, you may wish to consider purchasing a download license of The TCP/IP Guide. Thanks for your support! Donate $2 Donate $5 Donate $10 Donate $20 Donate $30 Donate: $

---

Home - Table Of Contents - Contact Us

The TCP/IP Guide (http://www.TCPIPGuide.com)
Version 3.0 - Version Date: September 20, 2005

© Copyright 2001-2005 Charles M. Kozierok. All Rights Reserved.
Not responsible for any loss resulting from the use of this site.